Эта статья - продолжение цикла переводов, посвященных геометрии и тому, как она работает в искусстве. Сегодня говорим о базовых формах и вспоминаем школьные уроки. Материал может показаться слишком простым, но без него будет сложно объяснить построение паттернов, которым посвящены остальные части.
О терминах и инструментах можно прочитать в первой части.
Обозначения на схемах
На учебных иллюстрациях в этом курсе используются следующие обозначения:

Треугольник (с заданной стороной)
Шаг 1
Начертите отрезок АВ. Он станет основанием треугольника. Раскройте циркуль на дину отрезка, установите иглу циркуля в А и проведите дугу через точку В.
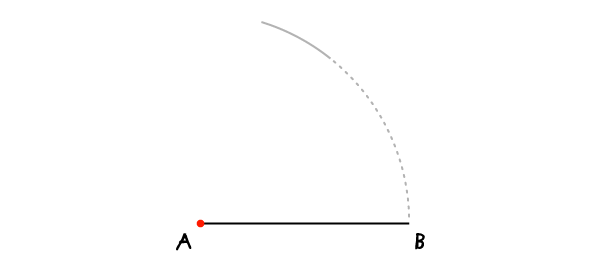
Шаг 2
Не меняя раскрыва циркуля, установите иглу в точку В и проведите дугу через точку А. Так вы получите точку С.
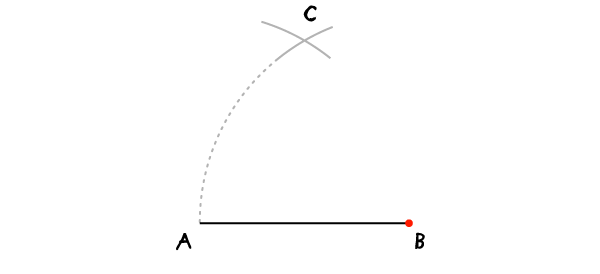
Шаг 3
Соедините точки А, В и С – и получите равносторонний треугольник. Если раскрыв циркуля больше или меньше основания АВ, то треугольник в результате получится равнобедренным.
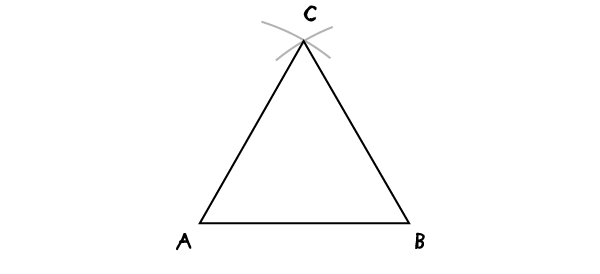
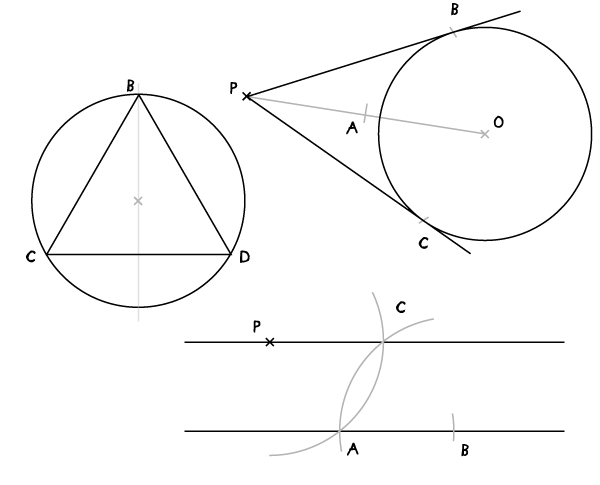
Треугольник (вписанный в круг)
Шаг 1
В предварительно начерченной окружности через центр проведите линию, соединяющую А и В.
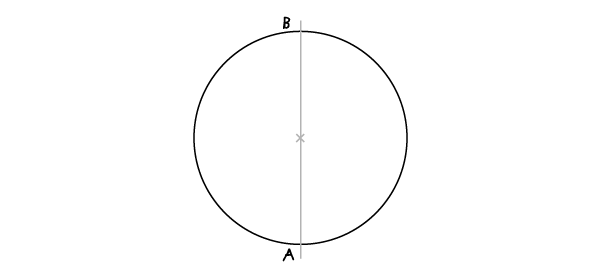
Шаг 2
Не меняя раскрыва циркуля, проведите дугу, которая пересечет окружность в точках С и D.
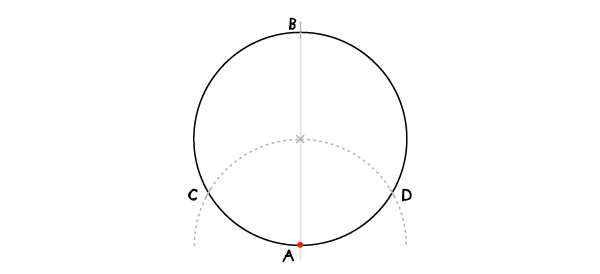
Шаг 3
Соедините точки B, C, D.
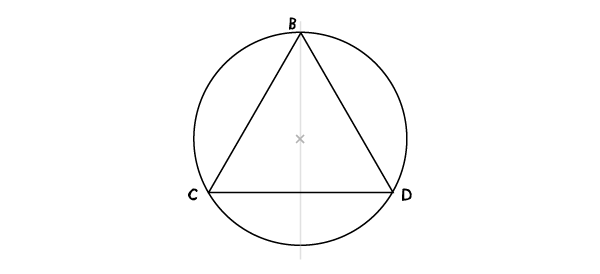
Биссектриса (перпендикуляр)
Наукообразный термин означает линию, которая обладает двумя свойствами: делит отрезок (или угол) на две равные половины и является перпендикулярной к делимому отрезку. Эта линия – важный инструмент, который часто используется в ходе построения других фигур.
Шаг 1
Установите иглу в точку А и с раскрывом циркуля АВ проведите дугу.
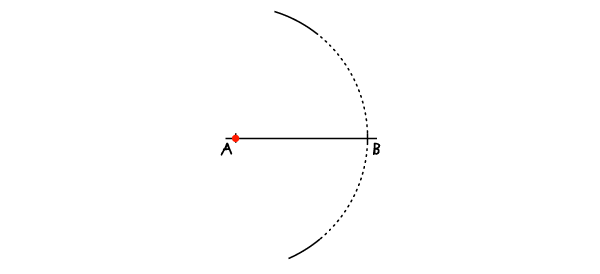
Шаг 2
Повторите для точки В так, чтобы дуги пересекались в двух точках.
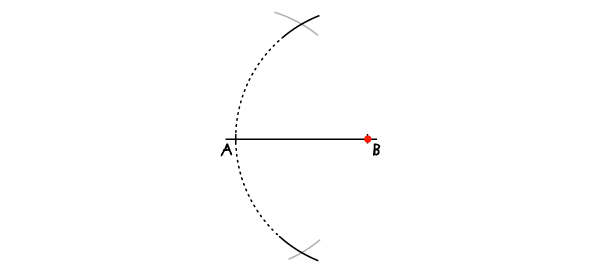
Шаг 3
Проведите линию через точки пересечения дуг. Точка О, в которой линия пересечет отрезок, будет серединой отрезка.
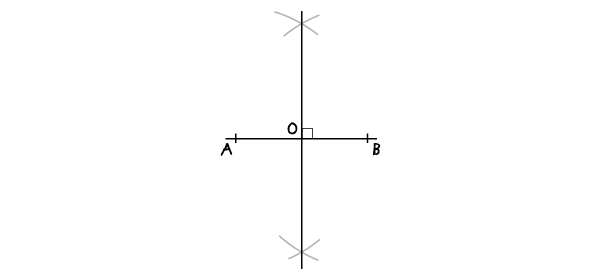
Касательная к окружности в заданной точке
Если на окружности есть точка (Р), через которую вам нужно провести касательную, то:
Шаг 1
Для начала проведите диаметра через Р и О (центр окружности), он пересечет окружность в точке А.
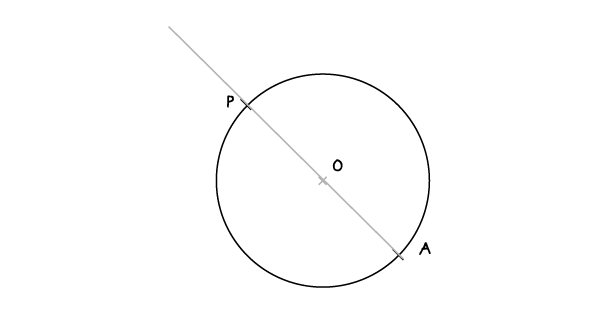
Шаг 2
Раскройте циркуль на ширину, равную отрезку АР, установите иглу в точку О и проведите большую дугу, почти полуокружность. Продолжите прямую АР до пересечения с дугой, и получите точку В.
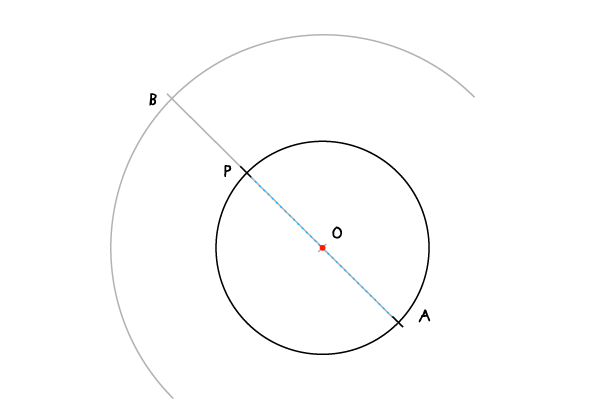
Шаг 3
Не меняя раскрыва циркуля, установите иглу в В и проведите дугу. Две дуги пересекутся в двух точках, С и D.
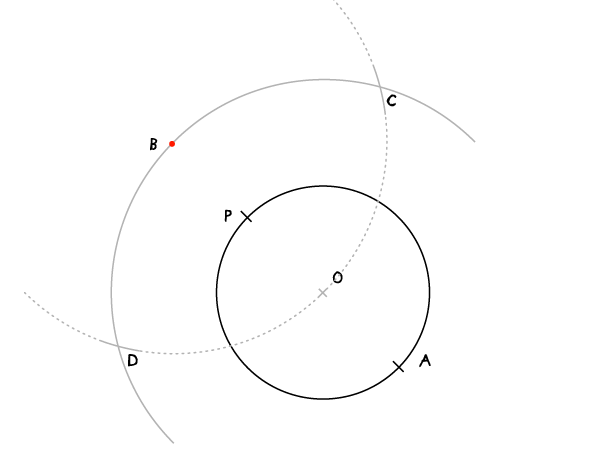
Шаг 4
Проведите прямую через С и D, это и будет касательная.
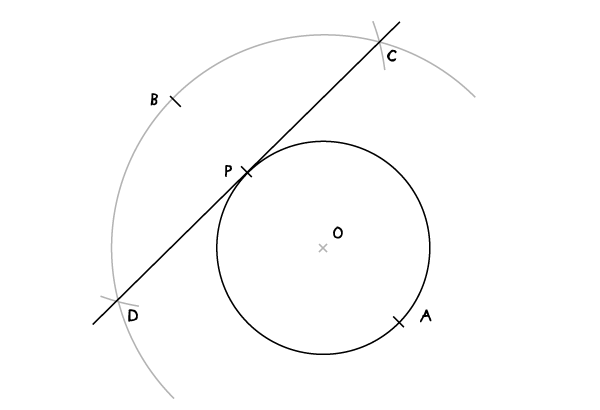
Касательная к окружности (через заданную точку вне окружности)
Пусть есть точка Р, лежащая вне окружности, и через нее необходимо провести касательную к окружности. Тогда:
Шаг 1
Начертите отрезок РО.
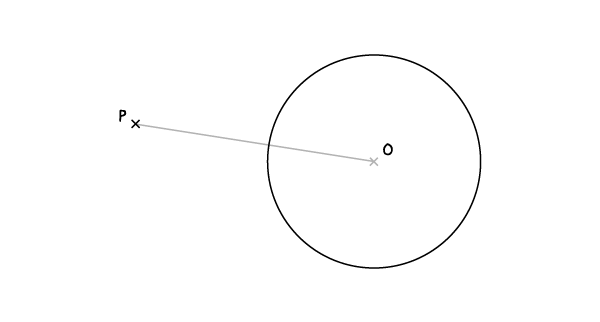
Шаг 2
Проведите перпендикуляр, делящий этот отрезок пополам.
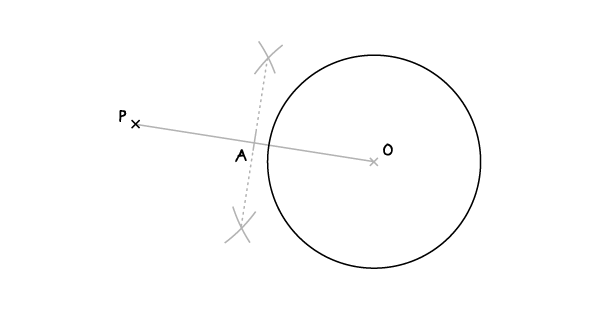
Шаг 3
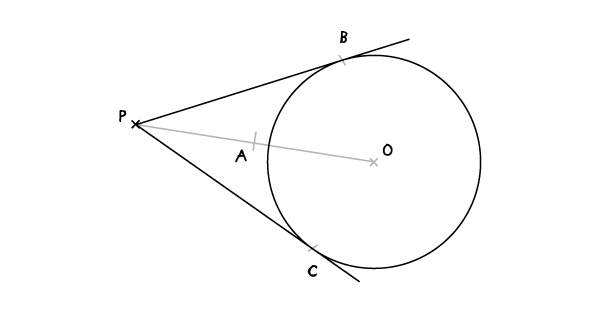
С раскрывом циркуля, равным АО, и иглой, установленной в точке А, проведите дугу, пересекающую окружность в точках В и С.
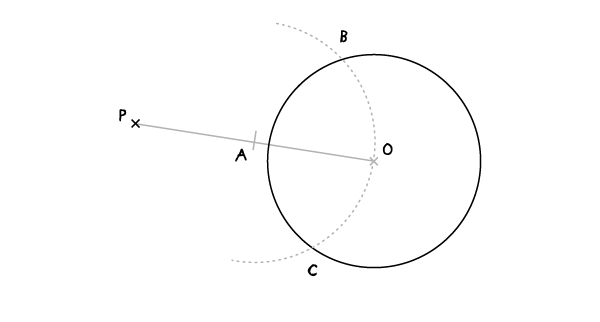
Шаг 4
Прямые РВ и РС – две возможные касательные к нашей окружности.
Параллельная прямая ( через заданную точку)
Параллельные прямые – такие прямые, которые никогда не пересекаются, поскольку идут в точности в одном направлении. Если вы учились в школе, то у вас в голове наверняка остались неясные образы того, как их строить. Хотя на самом-то деле рисовали вы их наверняка по клеточкам. Однако есть ведь правильный способ начертить действительно параллельные прямые!
Пусть у нас есть прямая, и точка Р, не лежащая на ней. Через эту точку и пройдет вторая прямая.
Шаг 1
Установите иглу в точку Р и проведите дугу, пересекающую данную линию в точке А.
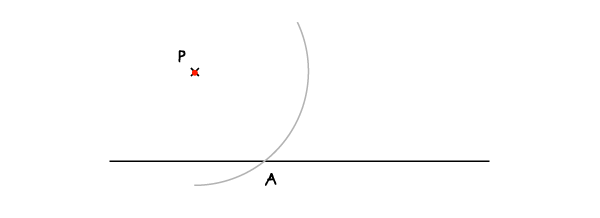
Шаг 2
Не меняя раскрыва циркуля, установите иглу в А и проведите дугу, пересекающую данную прямую в точке В.
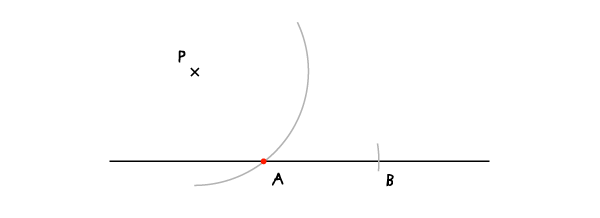
Шаг 3
Не меняя раскрыва циркуля, установите иглу в В и проведите вторую дугу, пересекающую первую в точке С.
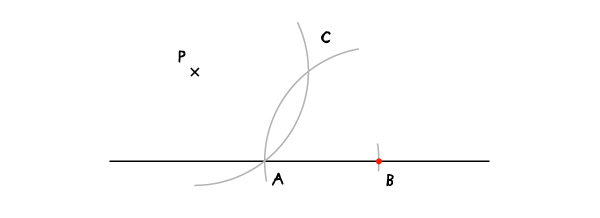
Шаг 4
Проведите прямую РС, она и будет параллельна данной
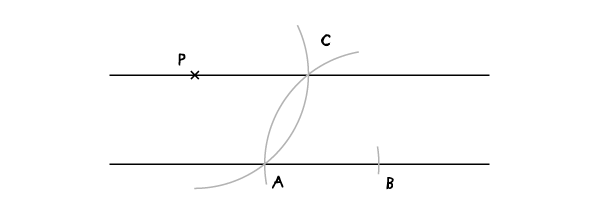
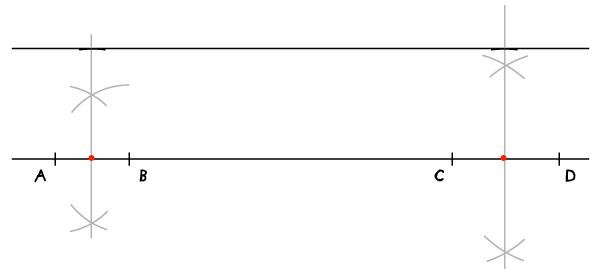
Параллельные линии (на заданном расстоянии)
Задача посложнее – построить прямую, параллельную данной и на определенном расстоянии от нее.
Шаг 1
Начните с того, что на данной прямой отметьте две пары точек. Расстояния роли не играют, но чем сильнее разнесены пары точек, тем точнее результат.

Шаг 2
Постройте два перпендикуляра, делящих отрезки между точками пополам.
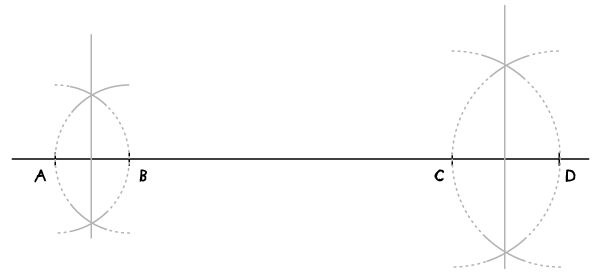
Шаг 3
Раскройте циркуль на ширину, равную нужному вам расстоянию между прямыми, и проведите дуги через оба перпендикуляра с иглой в серединах соответствующих отрезков.
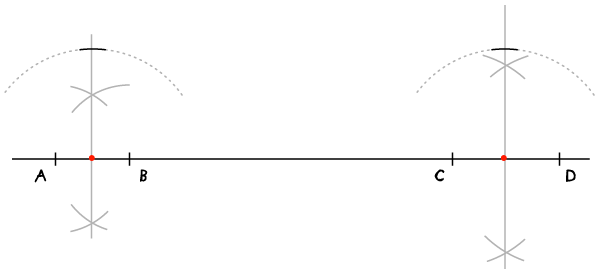
Шаг 4
Соедините точки пересечения дуг с перпендикулярами – это и будет прямая, параллельная данной.
Деление отрезка
Первое практическое занятие закончим изящным методом, позволяющим разделить отрезок на произвольное число равных частей. Он может быть полезен и когда у вас под рукой нет линейки со измерительной шкалой, и когда такая линейка бесполезна, если, например, у вас отрезок длиной 5.36 см, а разделить его вам надо на 7 частей. Этот метод точек и избавит вас от муторных вычислений.
В нашем примере разделим отрезок на 7 частей.
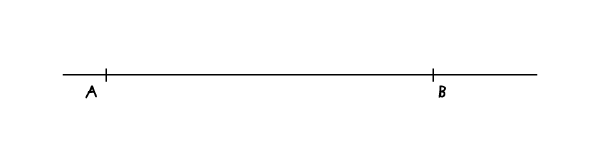
Шаг 1
Нарисуйте две дуги с иглой циркуля в точках А и В. Радиус неважен, главное, чтобы дуги пересекались в двух точках.
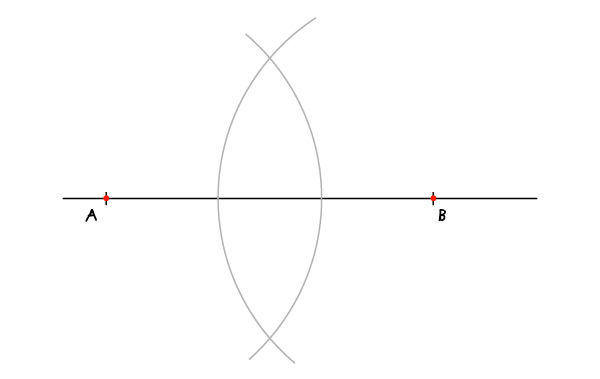
Шаг 2
Проведите две прямые: через точку А и одну из точек пересечения дуг и через точку В и вторую точку пересечения дуг.
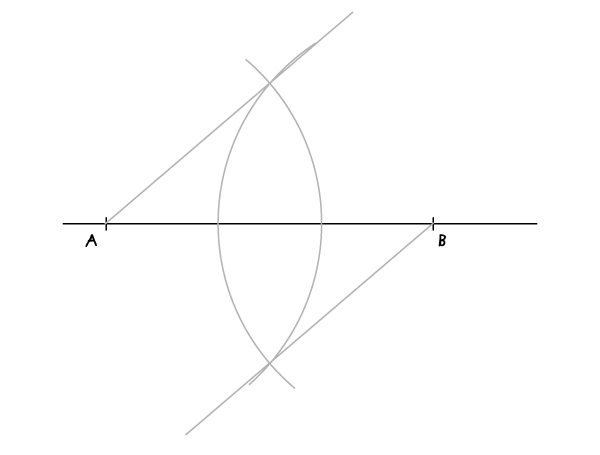
Шаг 3
Теперь на каждой из проведенных прямых наметим одинаковое число равных отрезков. Их длина неважна, но удобнее, чтобы они были поменьше – они должны уместиться на проведенных прямых. Их число равно N-1, где N– число сегментов, на которые нужно поделить отрезок, т.е. в нашем случае 7-1=6. На рисунке показан первым отрезок, построенный с иглой циркуля в точке А.
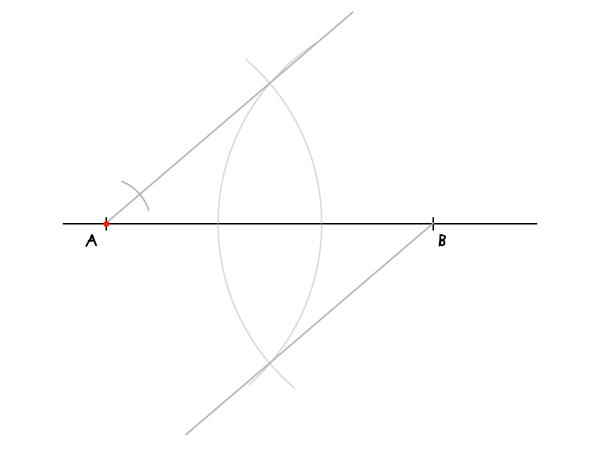
Шаг 4
Перемещайте иглу в каждую следующую полученную точку, пока не будет построено по 6 точек на каждой прямой.
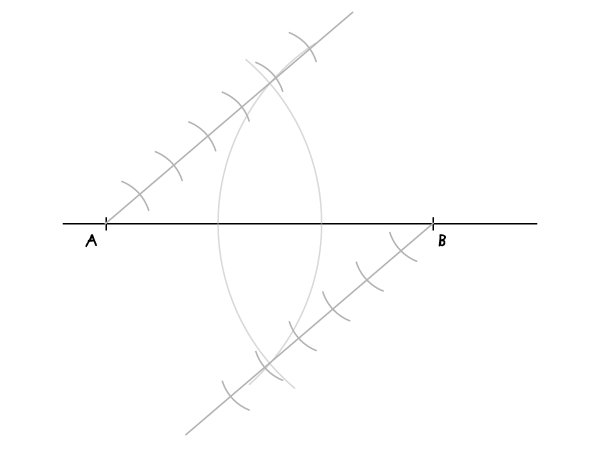
Шаг 5
Соедините точки как показано на рисунке, и получите данный отрезок АВ, разделенный на 7 равных частей.
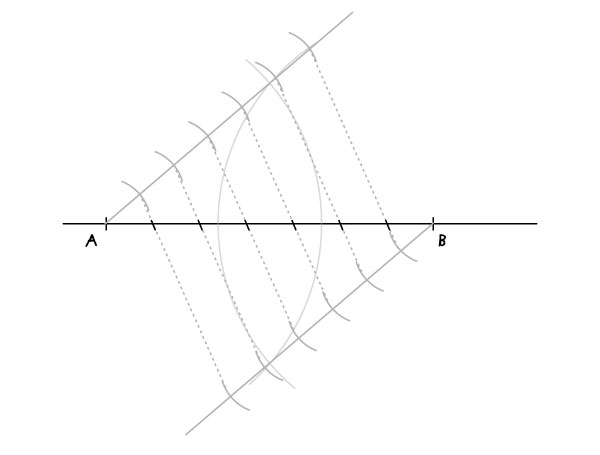
Что ж, мы сделали первый шаг в геометрии как искусстве, изучили базовые операции построения, которые в ближайших уроках найдут практическое применение (или могут быть полезны лично вам, если вы решите осваивать вопрос самостоятельно). В следующий раз перейдем уже к настоящим формам и узорам: на основе четырех- и восьмиугольников.